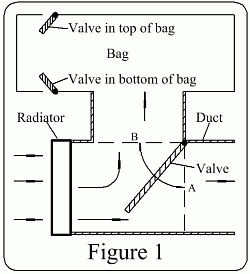
Figure 1
Airships use helium. To go up the bag (sometimes called the envelope) is filled. To go down some helium is compressed into small bags, called ballonets. Helium is getting scarce and expensive, and there are problems associated with the use of other gases. Hot air can be used instead of helium and such ships use a gas burner to heat the air. Here it is shown that airships can use air which is heated by the engines.
To ensure that the values used are realistic an example airship is used, currently made by HAV, the Airlander 10. Specifications are given in the appendix.
The engines of this airship are diesel, and a general rule of thumb is that the energy consumed by such engines is distributed thus: 35% power output, 35% exhaust & 30% water jacket. The power output of the example engines (four are used) is 1MW. This means that the heat from the water jacket is 895kW. This heat is available in the air leaving the engine radiators. Allowing for the inaccuracy of the rule of thumb, and for losses, assume that only 400kW is available.
Figure 1 shows how the air from the radiators can be directed into the bag, to raise the temperature of the air in the bag. The pressure in the bag is maintained at ambient pressure by a pressure relief valve releasing air from the top of the bag, so the density of that air is decreased, and the bag becomes buoyant.
Ambient air is drawn through the radiator as in normal practice. From the radiator the air, instead of escaping to atmosphere as normal, enters a duct. In the duct is a valve which can take any position between its extents A & B. At A all the air is directed into the bag. At B, the air is vented to the atmosphere. Any position between A & B can can be selected to control the rate of ascent.
To descend, the valve at the top of the bag can be opened and a valve at the bottom of the bag can be opened, thus letting ambient (cooler) air into the bag.
| ICAO, for the ambient air in the troposphere | |
|---|---|
| Psl | Standard pressure at sea level = 101325Pa |
| Tsl | Standard temperature at sea level = 288.15K |
| ρsl | Standard density at sea level = 1.225kg/m3 |
| Ht | Height of tropopause = 11000m |
| L | Temperature lapse rate = (Tsl -Tt) / Ht = 0.0065K/m |
| Pt | Pressure at tropopause = 22633Pa |
| Tt | Temperature at tropopause = 216.65K |
| g | 9.80665m/s2 |
| R | Universal gas constant = 8.31447J/mol.K |
| M | Molar mass of dry air = 0.0289644kg/mol |
| Rs | Specific gas constant = R / M = 287.048J/kg.K |
In the lower stratosphere (constant T): Hs = Height above HT
| a | ambient |
| b | air in bag |
| f | final |
| i | ingoing air |
| o | out |
| m | mass = V.ρ kg |
| Vb | Volume of bag |
| Vs | Volume of ship, say = Vb |
| Wb | Weight of air in bag = Vb.ρb.g |
| Ws | Weight of (rest of ) ship |
| Wt | Wb + Ws |
| ρs | Density of ship = Wt / Vb |
| C | specific heat, kJ/kg.K |
| T | temperature, K |
| V | volume |
Upthrust = ρa g Vb
Acting against this is Wt
So total buoyancy force = ρa g Vb - Wt
For constant height: ρa g Vb = Wt
As stated above, Pb = Pa.
Example: required height = 500. From HAV's Airlander 10, Vb = 38000 & Ws = 20000.
If the bag is internally lined with Aerofoam or survival blanket material, then the thermal conductivity, λ, of the bag will be 0.044W/m2.K:
Heat loss = Surface area . δT . λ
≃ 15050 x 11 x 0.044
= 7.3kW
Example: required height = 6000.
Heat loss = 11.3kW
Example: required height = 11000.
Heat loss = 25.2kW
As shown above, 400kW is available. This is ample.
Regarding the air from the radiator: Cair ≃ 1.
Vb = 38000.
At sea level: ρa = 1.225, mb = 46550.
So the air from the radiator can raise the bag temperature by
At a temperature of 288 + 8.6,
In other words, a climb rate of 136m/min.
At H = 500: Pa = 95458 & Ta = 285
mb = 44346.
So the air from the radiator can raise the bag temperature by
At a temperature of 285 + 9,
In other words, a climb rate of 582m/min.
At H = 11000
Pa = 22663
Ta = 217
mb = 13828.
So the air from the radiator can raise the bag temperature by
At a temperature of 217 + 29,
In other words, a climb rate of 1184m/min.
The engine power will decrease with altitude, but power reduction is not considered here.
So far the heat from the water jacket has been considered, but more heat is available from the exhaust. It is not suggested that the exhaust is vented into the bag, which would cause contamination of the bag material and internal components. Instead, the heat from the exhaust can be used as shown in Figure 2.
The exhaust pipe is part of a duct with a valve which works as explained in Figure 1. With the valve in position B the exhaust is vented to atmosphere. When the exhaust is directed into the bag the flow is then through a heat exchanger and then is vented to atmosphere.
The use of heat from diesel engines is a practical proposition.
As airship speeds increase the use of jet engines will become practicable.
An example of a current engine of the required power output is the General Electric CT7. This has an air flow rate of 4.5kg/s, and the exhaust temperature will be ≃ 1073K. With four engines, and letting C = 1, the heat power available is 14.4MW. From Maintenance of Constant Height it can be seen that this is sufficient for the ceiling of the Airlander, 6000m. Figure 3 shows how to achieve the heat exchange.
The exhaust is ducted. The duct has two interconnected valves. With the valves at B the exhaust is vented to atmosphere. With the valves at A the exhaust heat is directed into the bag, the flow then being through heat exchanger and then to atmosphere.
Another way of getting heat from a jet engine, turboprop, turbofan or turbojet, is to take air from the compressor, as shown in Figure 4.
Some air is bled from the compressor outlet into a duct, 2, containing a valve, 3, which can move between the extents A & B as before. With the valve at B the air is redirected back to the engine, 4. With the valve at A the air is directed to the bag, 5.
The compression is isentropic and a CR of 4 is typical of current engines. γ for air = 1.4.
At sea level: Ta = 288 & Pa = 101325.
At 500m: Ta = 285 & Pa = 95458.
For an ascent between these heights let Ta & Pa be the median values, ie, 286.5 & 98392.
From the compressor: Po = 685238, To = 499 & ρo = 4.78
From Maintenance of Constant Height:
For a mixture of two masses of air at different temperatures:
Once the masses are mixed the composition will be:
( Va - Vi ) @ 288K + Vi @ 499K
To match the rate of ascent accomplished by the radiator air of the diesel-powered ship, Vi must be supplied in 221s.
(presuming four engines). Such an engine can be made.
The use of heat from a jet engine is a practical proposition.
For maintenance of height there is no difference. For rate of climb, the density of helium at STP is 0.179kg/m3, so helium is far superior. The other advantage of helium becomes apparent when considering a cold start. When using air, first the engines must be warmed up and then the air in the bag must be heated. There is a patent covering the use of engines to heat the gas in the bag, but I suspect that the cold start is the reason that hot air is not used.
| HAV Airlander 10 | |
|---|---|
| Bag volume | 38000 |
| Length | 92 |
| Width | 43.5 |
| Height | 26 |
| Endurance | 5 days manned |
| Altitude | 6100 |
| Engines | 4 x 261kW, 4 litre, turbocharged diesels |
| Total weight | 20000 |
| Payload | 10000 |
| Speed | cruise 41, loiter 10 |
| GE CT7 turboprop engine | |
|---|---|
| SHP | 1100kW |
| Air flow | 4.5kg/s |
Howard's Stuff Index
Back to Pigeon's Nest
Be kind to pigeons